Here is my series of videos that I produced with the New Media Center of the University Basel for the Linear Algebra II course in spring semester 2017.
This mindmap gives a short overview how the videos are related:
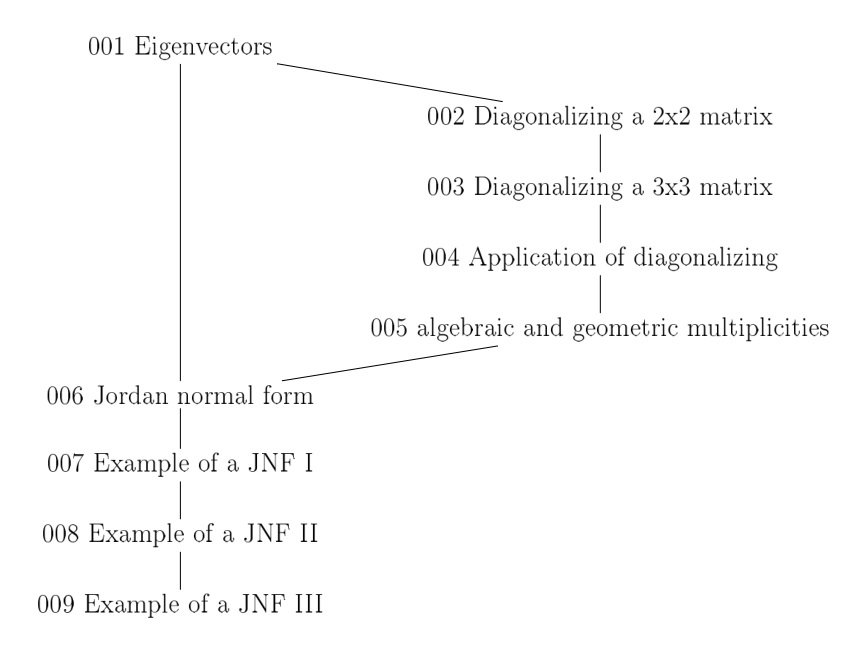
001 Eigenvectors
We will define eigenvalues, eigenvectors and the eigenspace. We will learn the link between the characteristic polynomial and the eigenvalues.
You can find the screenshot here.
002 Diagonalizing a 2×2 matrix
We will diagonalize a 2×2 matrix by computing the eigenvectors.
You can find the screenshot here.
003 Diagonalizing a 3×3 matrix
We will diagonalize a 3×3 matrix by computing the eigenvectors.
You can find the screenshot here.
004 Application of Diagonalizing
We will find an iterative formula for a recursive law by using matrix diagonalization.
You can find the screenshot here.
005 Algebraic and geometric multiplicities
We will define algebraic and geometric multiplicities, see how they are related and define the generalized eigenspaces.
You can find the screenshot here.
006 Jordan normal form
We will define the Jordan normal form and describe an algorithm to find the corresponding base change matrix.
You can find the screenshot here.
007 Example of a Jordan normal form
We will compute the Jordan normal form and the base change matrix for a matrix with one eigenvalue and one Jordan block.
You can find the screenshot here.
008 Example of a Jordan normal form
We will compute the Jordan normal form and the base change matrix for a matrix with one eigenvalue and two Jordan blocks.
You can find the screenshot here.
009 Example of a Jordan normal form
We will compute the Jordan normal form and the base change matrix for a matrix with two eigenvalue and two Jordan blocks.
You can find the screenshot here.